|
| |||
|
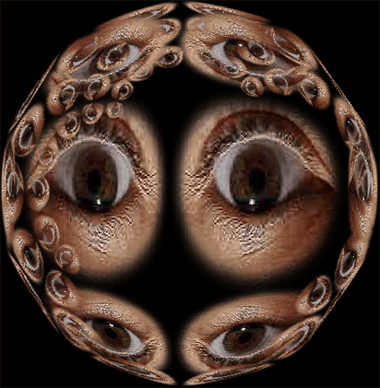
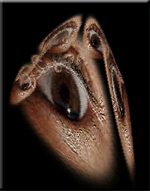
Olá Frédéric, "Oeil Complex" tem presença e caráter. E mistério. Adoraria dar uma olhada no seu código fonte. Veremos se Fred o revela para mim. Mas mesmo que ele não mostre o código fonte, o interesse real está no seu mistério e nele estar situado no interior da mente, como uma entidade da mente, como uma entidade que surge de uma meditação dos sólidos platônicos e o modo como as peças se juntam em formato 3D no espaço. A peça é profundamente intelectual, embora as crianças possam adorá-la. Existem apenas cinco sólidos platônicos: o tetraedro, o cubo, o
octaedro, o dodecaedro e o icosaedro. Cada face tem a mesma forma e
o ângulo entre duas faces contíguas é o mesmo que
existe entre quaisquer outras duas faces contíguas. Os sólidos
platônicos foram descritos por Platão no Timaeus cerca
de 350 AC. Platão comparou o tetraedro com o "elemento"
fogo, o cubo com a Terra, o icosaedro com a água, o octaedro
com o ar, e o dodecaedro com o material de que são feitos as
constelações e os céus. Ele também deveria
ter o conhecimento de que haviam somente cinco deste tipos de formas
possíveis (no espaço Euclidiano). | |||
|
Durieu
|
Olá, Andrews Sinto muito pela demora, mas estava muito muito muito ocupado. Sinto muito também pelo meu inglês ruim. Também agradeço pelo seu interesse no meu trabalho. Não é a primeira vez que alguém me faz tantas perguntas sobre o código fonte de "Oeil Complex"... Amo sua tentativa de explicá-lo, mas esta não
é uma boa direção. O código é muito muito simples... Não posso dá-lo para você, mas se você é um matemático pode achar a solução facilmente. Pense no nome da peça... | ||
|
Andrews |
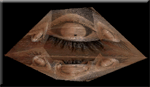
Oops. Provavelmente então não está relacionado com os sólidos platônicos! Se eu clicar "Oeil Complex" até obter a colméia sem globos oculares, "Oeil Complex" revelará a sua estrutura mais prontamente: todos os elementos são quadriláteros, enquanto que os sólidos platônicos são o cubo com faces quadradas; o tetraedro, o octaedro e o icosaedro com faces triângulares; e o dodecaedro com faces pentagonais. Imagino ser por isso então que existe essa possibilidade de interação: o ato de clicar conduz diretamente à percepção da estrutura. Quando você fez "Oeil Complex"? | ||
|
Durieu |
O código foi criado em 1999. | ||
|
Andrews |
Que tipos de assuntos você quis tratar nele? | ||
|
Durieu |
É um tipo de estranha criatura vivendo num mundo diferente. Nosso mundo é 3D; "Oeil complex" vive num mundo de 2.5D ouuuuu. É um plano tentando conquistar a terceira dimensão... | ||
|
Andrews |
Como você vê essa criatura que criou? | ||
|
Durieu |
Gosto muito dela porque é muito estranha, tão viva. Também porque o seu código é muito simples. Sou muito orgulhoso disso...Espero que "isto ou ele/ela" ? tenha sucesso em seu objetivo de alcançar o 3D... | ||
|
Andrews |
Para você, qual a personalidade dela? | ||
|
Durieu |
Não sei. Fiquei tão surpreso quando encontrei esta criatura. Ela nunca falou comigo. Penso que é muda. Parece talvez um pouco desesperada. | ||
|
Vejo isto muito bem realizado artisticamente, em relação
à programação e à matemática. E tão
engraçada também! Na minha opinião está
situada entre o reino das formas e este nosso mundo. Combina arte, matemática
e programação graciosamente. Mas principalmente tem uma
presença intrigante e inteligente como uma obra de arte. | |||
|
Durieu |
Ótimo trabalho, Jim. Você já tentou fazer um módulo interativo com ele? | ||
|
Andrews |
Não. Estava usando principalmente "Photoshop" e "CorelPaint" para fazer as peças, e um pouco de Java, naquele momento, em 96. O papel da matemática no seu trabalho é fascinante para mim, Fred. | ||
|
Durieu |
Gosto do poder da matemática. Mas sempre tento esconder este aspecto no meu trabalho. A matemática é somente uma ferramenta fácil para construir meus brinquedos. (Digo brinquedo em vez de jogo porque não gosto de aplicações onde é necessário vencer.) | ||
|
Andrews |
Sim, bem, os matemáticos inventaram computadores e a matemática é extremamente útil para a arte digital, como o seu trabalho indica - ou para qualquer arte na qual a construção envolva algum tipo de amena engenharia para a análise matemática. Você concordaria? | ||
|
Durieu |
Certo. Matemática é tão fácil de traduzir em código para computador. Para mim é o caminho mais simples para fazer animações na tela. | ||
|
Andrews |
Quais são as suas áreas favoritas na matemática? Você tem graduação em matemática? Qual é a sua formação, Fred? | ||
|
Sou engenheiro (o nome real na Bélgica é engenheiro civil, a escola é semelhante à escola politécnica na França). Meu interesse principal não é realmente a matemática, mas a maioria do tempo uso as leis da cinética (física) para mover coisas com aceleração e fricção. Gosto muito do fato de não precisar ser exato (matematicamente falando) no meu trabalho. Somente o efeito final na tela é importante. Algumas vezes, erros ou efeitos colaterais no código dão excelentes resultados. Exatamente o contrário do que aprendi nos meus estudos. O que você pensa de "puppettool"? É meu trabalho principal agora e me dá muito prazer. | |||
|
Andrews |
Eu o compararia com sodaplay.com , o qual você provavelmente conhece. Suas criaturas possuem mais graça do que as criaturas do 'sodaplay", eu diria. | ||
|
Durieu |
Conheci esse artista em Paris. Seu trabalho é ótimo. Penso que esteja entre os melhores da internet. | ||
|
Andrews |
Você está explorando uma fronteira entre a ferramenta e a obra de arte. Você considera" Puppettool" um trabalho de arte ou uma ferramenta? Ou uma mistura? Você pensa que há tensão entre a idéia de ferramenta e a idéia de trabalho de arte? | ||
|
Durieu |
Para mim é uma ferramenta para definir estados do "puppet" (boneco, marionete). Antes dessa ferramenta era muito difícil fazer isso. Para as girafas, tive que colocar todos os coeficientes em uma incrível ordem! Mas agora é também um lugar de criação. Recebi 500 estados de diferentes usuários e alguns são incríveis, realmente peças de arte. Então "Puppettool" talvez esteja na fronteira entre ferramenta e obra de arte. | ||
|
Andrews |
Sei que o seu "Puppettool" está sendo cotado para o "prix transmediale" (prêmios de obras transmidiáticas), Fred-"bon chance" (boa sorte)! | ||
|
Durieu |
Você está bem informado! Obrigado! | ||
|
Andrews |
Você considera que o seu trabalho "Zoo" seja mais popular que "Oeil Complex"? Se a resposta for positiva, por que isto acontece, você sabe? | ||
|
Durieu |
Sim, o "Zoo" tem tido um enorme sucesso. Provavelmente porque os animais são mais acessíveis (realistas)? | ||
|
Andrews |
Este trabalho é uma extensão do trabalho "Oeil Complex" ou é totalmente diferente? | ||
|
Durieu |
É um trabalho totalmente diferente, mas, como todos os meus trabalhos, é sempre repleto de leis da matemática e da física. | ||
|
Andrews |
Como você descreveria suas principais preocupações como um artista programador? | ||
| Estou usando muitos algoritmos complicados, mas o objetivo de tudo isso é criar poesia. Então, gosto de falar de poesia algorítmica. Um poema é um texto que lhe oferece poesia se você o lê. O código que estou tentando escrever é um texto que lhe oferece poesia se o computador o decifrar.... | |||
|
Andrews |
Ha Ha Ha! Sim, você dá ao computador um trabalho interessante para fazer, o que não acontece freqüentemente. Tal arte é incompreensível para a maioria—embora a maioria possa apreciar a leitura do computador.
| ||
|
Durieu |
Gosto de "week-end" , do "Zoo" e dos atalhos do "Puppettool" em: www.LeCielEstBleu.com/weekend www.LeCielEstBleu.com/zoo www.LeCielEstBleu.com/puppettool Um dos meus melhores trabalhos é o CDROM "Alphabet", 15 prêmios mundiais.... É a compilação de 50 telas interativas ("Oeil Complex" e outros gráficos estão no CD "Alphabet" junto com uma peça onde se usa um microfone). "Amazon" o vende na América do Norte (É um produto Tivola)—Dadamedia.com o vende na Europa. Enquanto trabalhava no "Alphabet", encontrei Jean-Jacques Birgé. Foi realmente um prazer trabalhar com ele em música interativa. Ele é incrivelmente criativo e nós ainda trabalhamos juntos regularmente no "LeCielEstBleuBleu". | ||
|
Andrews |
Noto que você, Antoine Schmitt e Nicolas Clauss parecem compartilhar um interesse no que se refere ao movimento em programação. Isto é algo que você conversa com eles? | ||
|
Durieu |
Antoine Schmitt é um programador maravilhoso (ele já trabalhou para a NeXT). Mas, quando o vejo, raramente nós conversamos sobre programação. Nicolas Clauss não é realmente um programador mas um pintor que substituiu seus pincéis pelo "software" "Director". Nós nos encontramos há dois anos atrás, depois que ele tomou conhecimento do "Alphabet". Eu mostrei o "Director" para ele. Nós nos tornamos amigos rapidamente e algum tempo depois ele começou a construir o seu lindo "site" "flyingpuppet". | ||
|
Andrews |
Que outras preocupações e interesses você compartilha com Schmitt, Clauss, servovalve e Jean-Luc Lamarque? | ||
|
Durieu |
Em Paris existem muitos eventos em torno de novas mídias... e festas. Nós gostamos de conversar sobre os projetos que nós estamos fazendo. | ||
|
Andrews |
Todos vocês usam "Director' e são artistas-programadores. Como aconteceu isto? | ||
|
Durieu |
O "Director" continua sendo "A" ferramenta para fazer interatividade. A linguagem é tão flexível, tão fácil e tão poderosa. Schmitt , Lamarque e eu usamos "Director" há muito tempo (dez anos). Falo Lingo (linguagem de programação do 'software' 'Director') como falo francês. | ||
|
Andrews |
Você pensa não ser habitual o fato de fazer parte de um grupo assim talentoso, todos utilizando a mesma ferramenta e sendo artistas da "web" na mesma vizinhança? Isto parece esplêndido aos meus olhos. | ||
|
Durieu |
Penso que há muitos artistas usando 'Director' no mundo. Não vejo a situação como não habitual. Talvez porque nós estejamos vindo do mundo do CD-ROM (agora morto). É um tipo de reorganização para a "Web". | ||
|
Andrews |
Qual é o seu emprego? | ||
|
Durieu |
Há ainda alguns CD-ROMs para programar em Paris. Participo em algumas exibições (em algumas delas recebo pagamento). Minha namorada Kristine Malden, da cidade de Nova Iorque, o olho no "Oeil Complex", trabalha comigo a maior parte do tempo. Nós criamos juntos o módulo "SetSearch" , um tipo de engenho para procurar música. Ela está fazendo também "web sites" ... Algumas vezes nós fazemos alguns módulos para outras companhias (nós estamos agora trabalhando com o "Nike sur des puppets" , - dê uma olha no "mp3 player". | ||
|
Andrews |
Quanto tempo você trabalhou em "Oeil Complex"? | ||
|
Durieu |
Um tempo muito curto. Um dia. | ||
|
Andrews |
Um dia? Não posso acreditar! Qual o tamanho do código? | ||
|
Durieu |
141 linhas. Posso entender porque você não confia em mim... Penso que é porque você não entende como ele trabalha. Posso dar a você uma pequena ajuda. Você sabe números complexos em Matemática? |
||
|
Andrews |
Ah, um pouquinho. | ||
|
Durieu |
"Oeil Complex" é somente uma função muito simples (transformação do plano X-Y ). O estranho efeito 3D é somente cinco ou seis linhas de código. | ||
|
Andrews |
É isso uma projeção estereoscópica? Análise complexa foi apenas um momento na minha formação. E posso ter estado ausente das aulas naquele dia! | ||
|
Durieu |
Números complexos estão
num plano imaginário. O número imaginário é "i", onde i . i = -1. no módulo, i é o eixo vertical. |
||
|
Andrews |
Nunca fui muito bom em análise complexa, seja gentil, Fred. O que significa ter um eixo i? Usualmente o eixo real é z . Isto é sobre onde fui ajudado no curso. Os quatérnios* não estão distantes. Nota da tradução: "Do ponto de vista físico, o sistema dos números complexos é extremamente conveniente para o estudo dos vetores e das rotações do plano. Hamilton vislumbrou a possibilidade de um sistema de números análogo para o estudo dos vetores e das rotações do espaço tridimensional. Em suas pesquisas, considerou quádruplos ordenados (a, b, c, d) de números reais, tendo imerso neles tanto os números reais como os números complexos. Chamando esses elementos de quatérnios (reais), Hamilton definiu a adição e a multiplicação dos quatérnios, podendo verificar as propriedades associativas e comutativas da adição e que a multiplicação é associativa e distributiva em relação à adição, mas não vale a lei comutativa da multiplicação. Este é, historicamente, o primeiro exemplo de uma álgebra não-comutativa." |
||
|
Durieu |
Não é fácil explicar toda a teoria, mas aqui está a introdução para os números complexos: http://www.ping.be/math/complget.htm#The-complex-numbers. | ||
|
Andrews |
OK, eu li isto —eu tinha visto antes aquele material. | ||
|
Durieu |
Você conhece o conjunto "Mandelbrot" (fractal)? | ||
|
Andrews |
Somente dei uma olhada em http://math.bu.edu/DYSYS/MANDMAP/mandmap.html, então vi um pouco do que está acontecendo lá. | ||
|
Durieu |
O que fiz em "Oeil Complex" não está muito distante, mas tem uma função diferente e apenas uma repetição de computação. | ||
|
Andrews |
O "Mandelbrot" é um conjunto de números complexos que satisfazem uma certa condição. O seu é uma cartografia, usando coordenadas polares, de um quadrado (presumivelmente centrado na origem?) sob uma função complexa, onde a posição do "mouse" determina o valor do c e o argumento é um dos vértices do quadrado? | ||
|
Durieu |
bravo Estou impressionado. | ||
|
Ah ah, obrigado, obrigado. Gosto deste tipo de "puzzle" (quebra-cabeças) elegante, Fred. Ele é importante por ser matemática de alto nível a serviço da arte. Bravo por você criar tão maravilhoso trabalho! Estou ainda curioso sobre a natureza geral da função. Quanto mais olhos aparecem, mais a forma parece tender em direção à cartografia de uma esfera. Os poucos globos oculares, bem, a cartografia é esquisita e sugere os sólidos platônicos, entretanto eu sei que esta é uma abordagem errada. O que está acontecendo realmente? | |||
|
Durieu |
É só porque nós estamos trabalhando com os números complexos. Se você observar o quão é estranho o conjunto "Mandelbrot" e a complexidade de sua estrutura quando você o amplia. Não sei exatamente o tipo de formas que produz aqui. Parece ser uma esfera, mas não estou muito certo (se o número de facetas = infinidade). Muitas funções diferentes dão resultados muito bons (estranhos). | ||
|
Andrews |
Ah, agora posso entender o que você quer dizer, e isto é fascinante. Você está falando especificamente sobre funções complexas? Como você descreveria os tipos de funções a que você está se referindo? | ||
|
Durieu |
A função é 1/ (a+bi). Coisas simples são freqüentemente belas! Não? | ||
|
Andrews |
Mas sim! Merci, frère! | ||
|
Durieu |
O prazer foi meu, Jim. | ||
| |||